Pre-Calculus Notes

Today, I am tutoring a student in complex numbers, so I am going to use my journal to type up some notes before the study session:

• Polar Form of Complex Number:
• x + yj = r(cos0 + jsin0) where j = sqrt(-1)
• r = sqrt(x^2 + y^2)
• In polar form, 0 can be expressed as radians or degrees

*Radian = degrees * (pi/180)

*Degree = Radian * (180/pi)

*Euler's Formula: e^(ix) = cis(x) & e^(nix) = cos(nx) + isin(nx)

*0 = tan^-1(y/x) if x > 0 & 0 = tan^-1(y/x) + pi or 0 = tan^-1(y/x) + 180 degrees for x < 0

• De Moiver's Formula = z^n = r^n * cis(n0)
• ex:

**If z= 1 + j, what is z^10?

r = sqrt(x^2 + y^2) = sqrt(1^2 + 1 ^2) = √2

arctan(1/1) = tan^-1(1) = pi/4, so z = √2(cos(pi/4) + jsin(pi/4))

z^10 = √2^10 * cis (10 * pi/4) = 32cis(5pi / 2) = 32cis(2pi + (pi/2)) = 32cis(pi/2) = 32 (cos(pi/2) 0 + jsin(pi/2) 1) = 32j

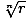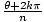*A complex number z = r(cos(θ) + ısin(θ) has exactly nnth roots given by the equation [cos() + ısin(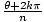)], where n is a positive integer, and k = 0, 1, 2,..., n - 2, n - 1.